Con lắc đơn có chiều dài $l=1(m)$ dao động điều hoà được treo trong một xe chạy trên mặt phẳng nghiêng góc $\alpha =30{}^\circ $ so với mặt ngang. Khối lượng quả cầu là $m=100\sqrt{3}(g)$. Tìm vị trí cân bằng, lực căng dây và chu kì dao động nhỏ của con lắc khi xe trượt không ma sát xuống mặt phẳng nghiêng.
Giải:
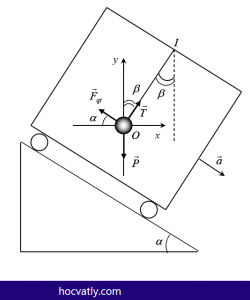
Khi xe trượt không ma sát xuống mặt phẳng nghiêng thì xe chuyển động nhanh dần đều với gia tốc: $a=g.\sin \alpha $
Ở vị trí cân bằng: $\vec{P}+\vec{T}+{{\vec{F}}_{qt}}=\vec{0}$ (*)
Chiếu (*) lên $Ox$: $T\sin \beta -{{F}_{qt}}\cos \alpha =0$ (1)
Chiếu (*) lên $Oy$: $T\cos \beta +{{F}_{qt}}\sin \alpha -P=0$ (2)
Từ (1) và (2)
$\Rightarrow \tan \beta =\frac{ma\cos \alpha }{-ma\sin \alpha +mg}$
$=\frac{g\sin \alpha \cos \alpha }{-g{{\sin }^{2}}\alpha +g}\Leftrightarrow \tan \beta =\frac{\sin \alpha \cos \alpha }{{{\cos }^{2}}\alpha }$
$\Rightarrow \tan \beta =\tan \alpha \Leftrightarrow \alpha =\beta $
Vậy khi con lắc ở vị trí cân bằng phương
sợi dây hợp với phương thẳng đứng gớc
$\alpha =\beta =30{}^\circ $, hay phương sợi dây vuông
góc với mặt phẳng nghiêng.
Lực căng dây:
Từ (1)$\Rightarrow T=\frac{{{F}_{qt}}\cos \alpha }{\sin \beta }=\frac{mg\sin \alpha \cos \alpha }{\sin \alpha }$
$=mg\cos \alpha =0,1.\sqrt{3}.10.\frac{\sqrt{3}}{2}=1,5(N)$
Ta coi con lắc dao động trong trọng lực hiệu dụng
$P’=mg’=T\Rightarrow g’=\frac{T}{m}=\frac{1,5}{0,1.\sqrt{3}}=8,66(m/{{s}^{2}})$
Chu kì con lắc là: $T’=2\pi \sqrt{\frac{l}{g’}}=2\pi \sqrt{\frac{1}{8,66}}=2,13(s)$
Was this helpful?
0 / 0