Bài viết này phù hợp cho các em học sinh lớp 10 khi học về cơ năng cũng như các em lớp 12 khi học về dao động điều hoà của con lắc đơn
NĂNG LƯỢNG CON LẮC ĐƠN – LỰC CĂNG DÂY
Chọn gốc thế năng ở vị trí cân bằng:
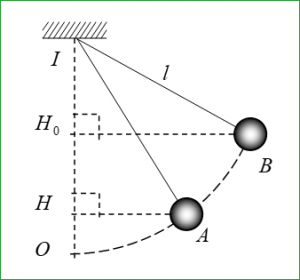
Cơ năng: $W={{W}_{}}+{{W}_{t}}$
Thế năng: ${{W}_{t}}=mgh$ với $h=l.\left( 1-\cos \alpha \right)$
Động năng: ${{W}_{}}=\frac{1}{2}m{{v}^{2}}$
- Ở biên độ B: ${{W}_{B}}={{W}_{\max }}=mg{{h}_{0}}$
với ${{h}_{0}}={{H}_{0}}O=IO-I{{H}_{0}}=l-l\cos {{\alpha }_{0}}=l.\left( 1-\cos {{\alpha }_{0}} \right)$
$\Rightarrow {{W}_{B}}={{W}_{t\max }}=mgl\left( 1-\cos {{\alpha }_{0}} \right)$
- Ở vị trí cân bằng O: ${{W}_{0}}={{W}_{\max }}=\frac{mv_{0}^{2}}{2}$
(với ${{v}_{0}}$ là vận tốc cực đại)
- Ở vị trí bất kì A: ${{W}_{A}}=mgh+\frac{m{{v}^{2}}}{2}$
với $h=HO=IO-IH=l-l\cos \alpha =l\left( 1-\cos \alpha \right)$
$\Rightarrow {{W}_{A}}=mgl\left( 1-\cos \alpha \right)+\frac{m{{v}^{2}}}{2}$
Tổng quát: cơ năng của con lắc
$W=mgl\left( 1-\cos {{\alpha }_{0}} \right)+\frac{mv_{0}^{2}}{2}=mgl(1-\cos {{\alpha }_{0}})+\frac{m{{v}^{2}}}{2}$
Ứng dụng của định luật bảo toàn cơ năng tìm vận tốc:
- Vận tốc khi con lắc qua vị trí cân bằng:
Gọi ${{W}_{B}}$ là cơ năng ở biên độ; ${{W}_{o}}$ là cơ năng ở vị trí cân bằng
Theo định luật bảo toàn cơ năng: ${{W}_{B}}={{W}_{O}}\Leftrightarrow mg{{h}_{0}}=\frac{mv_{0}^{2}}{2}\Leftrightarrow mgl\left( 1-\cos {{\alpha }_{0}} \right)=\frac{mv_{0}^{2}}{2}$
$\Rightarrow v_{0}^{2}=2gl\left( 1-\cos {{\alpha }_{0}} \right)\Leftrightarrow \left| {{v}_{0}} \right|=\sqrt{2gl\left( 1-\cos {{\alpha }_{0}} \right)}$
- Vận tốc khi con lắc ở A có góc lệch $\alpha $:
Theo định luật bảo toàn cơ năng:${{W}_{A}}={{W}_{B}}$
$\Leftrightarrow mgh+\frac{m{{v}^{2}}}{2}=mg{{h}_{0}}\Leftrightarrow {{v}^{2}}=2g\left( {{h}_{0}}-h \right)$
$\Rightarrow {{v}^{2}}=2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)\Leftrightarrow \left| v \right|=\sqrt{2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)}$
Ứng dụng của định luật bảo toàn cơ năng tìm lực căng dây:

- Lực căng dây T:
Theo định luật II Newton: $\vec{P}+\vec{T}=m\vec{a}$ (*)
Chiếu (*) lên phương sợi dây, chiều dương
hướng vào tâm, ta được:
$P\cos \alpha +T=m{{a}_{ht}}$$\Rightarrow T=m\frac{{{v}^{2}}}{l}+mg\cos \alpha $
Chứng minh để có: ${{v}^{2}}=2gl\left( \cos \alpha -\cos {{\alpha }_{0}} \right)$
$\Rightarrow T=3mg\cos \alpha -2mg\cos {{\alpha }_{0}}$
Ở vị trí cân bằng: $\alpha =0\Rightarrow {{T}_{\max }}=3mg-2mg\cos {{\alpha }_{0}}$
Ở vị trí biên: $\alpha ={{\alpha }_{0}}\Rightarrow {{T}_{\min }}=mg\cos {{\alpha }_{0}}$